原标题：roast世界咖啡新闻 |其他|达西定律与意式浓缩萃取

　　将达西定律应用到意式浓缩咖啡的制作中，我们可以理解为什么增加粉量会减慢水流经粉饼的流速；增加粉量使水在粉饼中渗透/流动距离变长，由此提升了粉饼的阻力。

　　Henry Darcy 在19世纪中叶通过直立圆筒装置中均匀沙土渗流实验得出了达西定律。达西定律仅仅适用于均质多孔介质中的流体在低速度、小孔隙、可渗透条件下的流动。

　　然而，在意式浓缩制作过程中水流却是快速地流过多孔介质（粉饼），为此我们需要了解一下达西定律。

　　达西定律

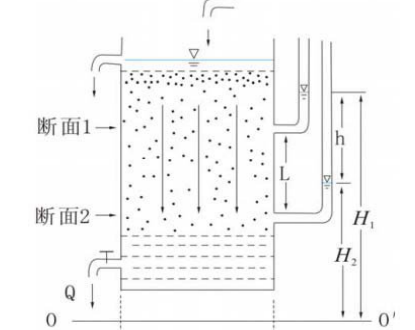
　　Q=K*A*（h1-h2）/L

　　Q为单位时间渗透流量，

　　A为过水断面面积，

　　△ h（H1-H2）为总水头差，

　　L为渗流路径长度，

　　i=△ h/L为水力梯度

　　K为介质渗透系数。

　　关系式表明，水在单位时间内通过多孔介质的渗流量Q与渗流路径长度L成反比，与过水断面面积 A和与水力梯度成正比;通过一断面的平均流速V=Ki,即渗透速度V与水力梯度一次方成正比。

　　(在实验中）圆柱的直径增加一倍，通过的水量就会增加一倍，而使圆柱的长度增加一倍，流速减半。压力加倍，流速也会加倍——但我们知道，在浓缩咖啡萃取过程中这种情况不会发生——为什么达西定律在浓缩咖啡萃取过程中不适用呢?

　　层流/紊流/雷诺数

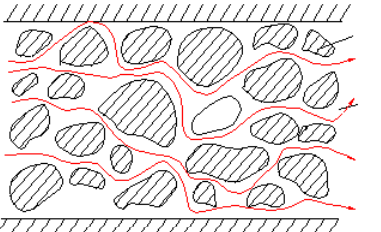
　　砂土中的渗透速度很小可以看作是一种水流流线互相平行的流动——层流

　　层流内水分子以平行直线形式通过

　　大量试验表明，在一般情况下，砂土、粘土中的渗透速度很小，其渗流可以看作是一种水流流线互相平行的流动——层流，渗流运动规律符合达西定律，渗透速度V与水力梯度i的关系可在v-i坐标系中表示成一条直线。

　　粗颗粒土（如砾、卵石等）的试验, 由于其孔隙很大，当水力梯度较大时，流速增大，渗流将过渡为不规则的相互混杂的流动形式——紊流,这时v-i关系呈非线性变化, 达西定律不再适用。

　　紊流

　　雷诺数

　　1883年英国人雷诺(O.Reynolds)观察了流体在圆管内的流动，首先指出，流体的流动形态除了与流速有关外，还与管径(d)、流体的粘度(μ)、流体的密度(ρ)这3个因素有关。

　　雷诺数Re=ρvL/μ，

　　ρ、μ为流体密度和动力粘性系数，

　　v、L为流场的特征速度和特征长度。

　　雷诺数较小时，粘滞力对流场的影响大于惯性，流场中流速的扰动会因粘滞力而衰减，流体流动稳定，为层流；反之，若雷诺数较大时，惯性对流场的影响大于粘滞力，流体流动较不稳定，流速的微小变化容易发展、增强，形成紊乱、不规则的紊流流场。

　　当雷诺数超过10时，紊流变得非常明显，达西定律不再适用。只有雷诺数（Re）≤1-10之间某一数值的层流运动才服从达西定律，超过此范围，V与i不是线性关系。

　　1901年Forchheimer根据试验资料得出非线性渗透定律，当渗透速度较大，雷诺数超过一定界限（大于10）时，渗透速度V与水力梯度i的平方根呈正比关系的，渗透速度V与水力梯度i的关系在v-i坐标系中表示成一条抛物线。

　　在浓缩咖啡制作过程中，快速流过粉饼的水的雷诺数要比流经砂土中水的雷诺数更高。

　　高流速下的紊流产生阻力，这意味着需要更多的压力才能达到预期给定的流速。因此，Forchheimer非线性渗透定律可以用于计算当流体是紊流时达到一定流速所需的额外压力。这意味着如果流速翻倍，由于紊流，压力需翻四倍。

　　根据达西定律，压力增加流速也会相应增加。然而，在浓缩咖啡制作过程中，情况并非如此——在一定程度下，增加压力反而会减少流速。

　　这里发生的事情是，增加压力实际上压缩了粉饼中颗粒之间的缝隙，降低了粉饼的渗透性。（这种效应在一般工程中称侧限压缩。常用不允许产生侧向变形的侧限压缩试验来测定土的压缩性指标以便测定各级压力作用下土样压缩至稳定时孔隙比的变化，据此绘制压缩曲线。）

　　达西定律在首次提出150多年后，仍被用作意式咖啡萃取模型的基础。然而，实际上萃取改变了流体流动形态，粘度和介质的渗透性，达西定律仅仅只能说明意式浓缩萃取过程中的一部分问题，而不是全部。（Roast杂志）